Subarticles:

Arndt source[edit]

Outline:

randomness
shourtcuts; monte carlo; misc; oddities
approximations: near fractions & continued frac
arctan; machin
spigot; computer continuous output
gauss; AGM
ramanujan
Borwiens
BBP: hex digit any; not decimal
arithmetic: FFT multip
misc / trivial / obscure
history: Aniquity (bible / india / babylon); polgyon/ infinite (add & mult) / high-perofrmance (rapid convernge?) / single digits
Misc: Indiana pi law / egypian pyramid size

Intro[edit]

p 3: feynman point: ps 768: six 9s consecutive; next group of six identical is at 193,034 ... also six 9s.
p 3: first zero appears a position 32.
p 3: first occurance of 0123456789 is at postion 17,387,594,880 ... later than expected
p 3: first position that is its own number is 1; another is 16,470 and 44,899. Arndt calls these "Self referential positions" Unknonw if there are infitite of these.
p 4: conjecture: Pi contains every finite sequenc eof numbers; including encoded bible, DnA of any individual, etc. Fact: BUT not infite e.g. sqrt(2).
p 4-5: not yet proven; normal or not? Appears to be normal. Not yet proven
p 5: hex representation also appears normal. Continued frction representation also shows no regularties (contrasted with e's CF with does have some patterns)
p 5: irrationality proven 1766 by J H Lambert.
p 5: 355/113 is a decent aproximatino, nown as early as 5th c China ... and was the best approximation until 13th c.
p 6: transcendental: proven in 1882 by F. Lindermann.
p 6: Amazing that very little has been proven about pi's characteristics since 1882.
p 6: "When one consides all the work that has been done on pi, the meagre amount that is known about it is somewhat surprising"
p 6: Proven transcendtal so far: pi**2; e**pi; ...
p 6: NOT yet proven irrational or not: e + pi; e * pi; pi / e; log(pi); pi**e
p 6: pi is "one of the oldest subjects of research by mankind" and "possibly the one topic within mathematics which has been researched the longest".
p 6: "Humans hvae concerned themselves with pi for several thousand years"
p 6: in 2000 BC, Babylonians and egyptians had approximations for pi that were 0.02 close
p 7: Squaring the circle: problem dates to 414 BC comedy The Birds by Aristophanes
p 7: STC: goal is to create a square with side s = r * sqrt (pi); using ONLY geometric constructions
p 7: STC finally shown impossible in 1882 by transcendental proof
p 8: inspite of STC disporven in 1882, "mathematical cranks" continue to try to prove it continually, e.g. book publi 1983 titled "pi is rational"
p 8: definitinos of pi: (1) Circ/diamter; (2) Area / (r*r). (3) [page 10, not page 8] first zero of cosine() function == pi/2.
p 9: diagram to prove area = pi * r * r;
p 9: pi also appears in non-circle contexts. e.g. probability stuff
p 9-10: non-circle context: what is probability p that a coin tossed n times has equal # heads and tails? p approaches 1 / sqrt ( pi * n ) [for large n] ... see Wallis product
p 10: non-circle context: Normal distribution ... from that page: " A normal distribution is often used as a first approximation to describe real-valued random variables that cluster around a single mean value. The normal distribution is considered the most prominent probability distribution in statistics. "
p 10: noncircle context: scores of "abstract" integrals and limits ... see page 223 for list. pi = integral (...); pi = lim n-> infinty sum (k0/n) blah blah
p 11 "It is unlikely that there have been as many pi enthusiasts as there are today" examples: large number of Web pages devoted to pi.
p 11: web sites of well known pi studers: Kanada and Borwein brothers.
p 11: Pi clubs exists
p 11-12: Holds a similar fasciation as the number "e" .. rather close to pi, and also transcen. But e is "relatively recent discovery" about 400 yrs old; 10 is 10x older; "e" has been computed to far fewer digits than pi;
p 12: Pi has been computed to 200 billion ( 2 * 10**11 ) digits as of year 2000. [larger since book publishd]
p 12: pi has been computed to more digits than any other constant. Other constnats as of yr 2000: 1/pi: 200 billion; sqrt(2) 137 billion; e (200 million);Apéry's constant aka ζ(3) 128 million digits; ln(2) 108 million digots.
p 12: individual digits are known beyond the 200 billion didgits, in hexadecimal system, e.g. 10 trillionthe digit. is an "A". Using a new techanique establish in 1995.
p 13: fame of pi may be related to the many "gandious formulae" for pi which are "an art". aka beautiful to mathematically inclined persons. Samples on page 13-14 chronol order:
- Viete's formula multipl from 1593 Viete#Works includes formla
- Lord William Brouncker in 1658: William_Brouncker,_2nd_Viscount_Brouncker#Brouncker.27s_formula includs forml
- arctan: from John Machin in 1706 ${\frac {\pi }{4}}=4\,\arctan {\frac {1}{5}}-\arctan {\frac {1}{239}}\!$
- Ramanujan 1914 ${\frac {1}{\pi }}={\frac {2{\sqrt {2}}}{9801}}\sum _{k=0}^{\infty }{\frac {(4k)!(1103+26390k)}{(k!)^{4}396^{4k}}}\!$
p 13-14: But the most famous formula of all is Euler's identity from 1743 $e^{i\pi }+1=0\,\!$
p 14: but, there is a formula relating e to pi without imagineary numbers:

{\frac {e+1}{e-1}}=2+4\sum _{r=0}^{\infty }{\frac {1}{(2\pi r)^{2}+1}}=0.

p 14: Popular culture: Carl Sagan's novel Contact
p 15-17: history of calculation of pi has 3 phases: (1)antiquity to 1630; archimedes & polygons; (2) mid 17th c -> 1980: infinite series, esp arctangent forumlae; (3) modern era: combined three techniques: (3a) Fast Fourier multiplication Multiplication_algorithm#Fourier_transform_methods; (3b) rapidly converging infinite series for pi (not based on arctangnet ) e.g. from B brothers Peter Borwein and Jonathan Borwein; or from Chudnovsky brothers; (or from Ramanujan ; or Guass's AGM). (3c) computer performance.
p 17: digits of pi exploded 1981 onward: 190% per year! "few other technologies have developed so rapidly"
p 17: What is motivation for calculating large number of digits? "beyond any practical need"
p 17: 39 digits is sufficient for diameter of universe to the nearest atom. Even if intermid calculations require more digits for round off issues, only "a few hundred digits" are needed by scientists and engineers
p 18: some practical benefits: (1) test computers; (2) a test number for numerical analysis (algotrihm setc): (3) learn more about pi (e.g. is normal or not)
p 18: human nature to try to break any record "every world record is crying out to be bettered"
p 19: Pi has an amazing ability to fascinate "Someone once said that one can turn a normal person into a pi fan, but that the reverse is not possible".
p 19: (new discorveries about) Pi acts a a showpiece for mathematics, in the eyes of the lay public. "pi is one of the rare objects in mathematics which act as a showpiece".
p 19: a big trend in pi research is computing digits "at the far end of pi" .. rather than recoputing the front digits.
p 19: this is possible due to the Bailey–Borwein–Plouffe formula [NOTE: this article calls it "a spigot algorithm" contrast with "the spigot algorithm" of ARndt
p 20: in 2000, Colin Percival created the PiHex distributed program (using a variant of the BBP formula) and spread it around thousands of volunteer's computers in the internet, and it computed (after 700 years of comptuer time) that the 250th trillionth hex digit of PI is hex E. (and hence the quadrillianth bit is zero).
p 20: As of today, these "far digit" algorithms only produce hex or binary digits ... not yet decimal.

CH 2 Random[edit]

p 21: define Normal number
p 22: not known if pi is normal or not
p 22: normal does not mean "no pattern" e.g. the number 0.1 2 3 4 5 6 7 8 9 10 11 12 .... is normal, but has a pattern.
p 22: Now that many digits of pi are known, statistical analysis can be done to evaluate normalness &randomness
p 23: "poker test" statistc: Statistical_randomness#Tests shows chi Sqrd restuls of 53% ... very random/typical
p 24-25: Martin Gardner remarked on some apparent patterns in first 32 digits of pi which give the appearance of patterns
p 25-26: e ** (Pi * sqrt (163)) had a very unusual propery: it is very, very near to integer: to right of decimal point is a set of twelve consectuie 9 digits!
p 25-26: this numer was "brougth to light" by Alexander Aitken in early 1900s. This is an example of several small numbers n (< 10,000) of form e**(pi*sqrt(n)) that is very, veyr near to integer. BUT wP article says "This number was discovered in 1859 by the mathematician Charles Hermite.^[1]"
May be more than coincidence. Unknown. See Mathematical coincidence
p 27: but almost certainly related to J-invariant#The_q-expansion_and_moonshine J-invariant
[no number] WP article Heegner number#Almost_integers_and_Ramanujan.27s_constant has detalis on this number
p 28-30: Yasumasa Kanada has used his digits of pi to do many statistical analyses: all consistent with random/normal; e.g. single digits are "very evenly distributed"
p 30-32: large number of pi digits available have undermined the arguments of some Intuitionism intuitionists such as Luitzen Egbertus Jan Brouwer because they relied on the incomputability of pi for some of their arguments (e.g. "does pi contain the digit sequence 1234567890"?)
p 32-33: what about non-decimal repre of pi? hex? CF?
p 32: e has a very strong pattern in its decimal CF.
p 33: deciaml CF appears to have no significant statistical meaning .."there .. is no other message than there is little regularity .."
p 33: another CF (not the standard CF) has: $=3+\textstyle {\cfrac {1^{2}}{6+\textstyle {\cfrac {3^{2}}{6+\textstyle {\cfrac {5^{2}}{6+\textstyle {\cfrac {7^{2}}{6+\textstyle {\cfrac {9^{2}}{6+\ddots }}}}}}}}}}$

[NOTE: the above is already in pi article]

p 33: "the known pi digits pass all random number teests with flying colours. For this reason one can use the digits of pi as a random number generator"

3 Shortcuts[edit]

p 35-36 Obfuscation programs: He gives a 1988 example by Brian Westley (not in WP) which is also at International_Obfuscated_C_Code_Contest#Examples which computes pi to 4 digits
p 37: Gives an example of a 133-character program in "C" that generates the first 15,000 chars of pi using the spigot algorithm of Stanley Rabinowitz and Stanley Wagon (not in WP).
p 37: Spigot algor was discoverd in 1991 by Rabinowitz
p 39: Monte Carlo methods - Comte de Buffon came up with Buffon's needle in 1777 - parallel lines & needles: ratio of hits to throws = 2:pi;
p 39-40: MC dartboard: ratio of hits (inside circle) to throws (inside circubscribed square) = pi / 4.

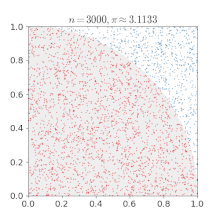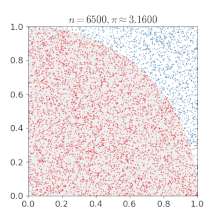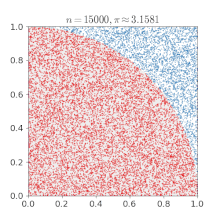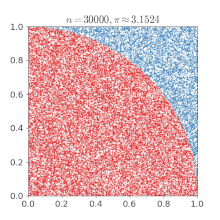
NOTE: this picture is no yet in pi article

p 41-43: the probability of two random numbers being relatively prime to each other = 6/ pi^2. See Coprime which has the formula etc. Arndt created a computer program to use this and after 1,000,000 pairs of numbers got pi=3.141554
p 43: monte carlo methods are simple and fun, but "they converge poorly ... probably the least efficient of all systematic procedures" for the calculation of pi.
p 44-45: mnemonic poems/verses for memorizing pi. E.g. 1905 in journal Nature a reader submitted one in English.
p 45: many languages have poems or similar mnemonics ... see main Piphilology
p 45: perhaps longest poe is "Cadaeic Cadenza" 3,865 digits of pi. by Michael Keith
p 47: memorizing: Not just oddballs: mathematician Simon Plouffe (coinventor of BBP algorithm) set memorization record in 1975 with 4,096 digits (broken 1977).
p 47: memorizing: current record data (obsolete)
(no page) memorizing: modern records: Akira Haraguchi - 100,000 digits; Lu Chao 67,890 digits. [1]
p 49-50: algorithm for calculating pi by _extending_ digits from a known (correct) baseline. Triple num correct digits each time. Popularized in 1961 by Daniel Shanks (who computed 100,000 digits of pi) but it was invented by Willebrord Snellius around 1600. If p0 is correct to n digits; then p1=p0+sine(p0) is correct to 3n digits.
p 50: trivia: pi room (salle pi) in Palais de la Découverte in Paris, 707 digits displayed in the wall

4 approxiaitons, esp CF[edit]

P 51-53; pi = 3; 22/7; 355/113
p 56: Plato: circa 400 BC pi = sqrt(2) + sqrt(3)
p 56: India Zhang Heng pi = sqrt(10)
p 56: Dante pi = 3 + sqrt(2)/10
p 61: trivia: pi^4 + pi^5 == e^6 (7 digits the same!! 403.4287)

5 Arc tan formulae[edit]

p 69: history: by 2000 BC Egypitans and Babylonians had arrived at 1 decimal place by physical measurement
p 69: history: Archimedes 250 BC was the 1st to use geometry (incribed polygons, etc) which was the primary method for coputing pi until 1630.
p 69: polygonal approximations got up to 39 digits
p 69: latter part of 17th c saw developemnt of infinite series and Infinitesimal calculus -> thus shift from geometrical solutions to analytical solutions
p 69: many infinite expressions for pi emerged. Some based on arctan
p 69: arctan series are relatively eacy to calculate: main one is called Gregory's series

\int _{0}^{x}\,{\frac {du}{1+u^{2}}}=\arctan x=x-{\frac {x^{3}}{3}}+{\frac {x^{5}}{5}}-{\frac {x^{7}}{7}}+\cdots

p 69: First European to discover the arctan series was James Gregory (mathematician) in 1671
[other books] However it was earlier discovered in Asia, probably by Mādhava of Sañgamāgrama;
[other] and documented in writing in 16th c by Nilakantha Somayaji
[other] orginally in verse, orally xmitted!!! in Sanskrit
p 70: plain arctan pi/4 converges very slowly, so alternatives were developed as in Euler's 1738 formula : ${\frac {\pi }{4}}=\arctan {\frac {1}{2}}+\arctan {\frac {1}{3}},$
p 72: in 1706 (before Euler) Machin came up with the Machin formula which got him to 100 digits

{\frac {\pi }{4}}=4\,\arctan {\frac {1}{5}}-\arctan {\frac {1}{239}}\!

p 72-74: machins is just one example of a whole host of similar formulat based on arctan, see Machin-like formula]

6: spigot algorithms[edit]

p 77: "The spigot algorithm for pi" was published by Stanley Rabinowitz and Stanley Wagon in 1995.
p 77: it differs from most other pi computation methods, such as the arttan methods, because it produces digits sequentially. The arctan algorithms require the user to fix a certain number of digits, compute several intermediate results, then combine the int resutls, to obtain a final result. No digits are prduced until the entire algorithm completes
p 77: very simple; also relatively fast: comparable to arctan algorithsm; but not as fast as AGM
p 84: also there is a spigot algorithm for e

7 Gauss and AGM[edit]

p 87 around 1809 by Carl Friedrich Gauss created the AGM method (using the Arithmetic-geometric mean - hence AGM) to create an algorithm to compute pi.
p 87: it is perhaps the fastest algorithm fo rocmputing pi
p 87: goes by several names: "Brent-Salamin iteration" or "Gauss-Legendre method" or "Gauss AGM algorithm".
p 87: algorithm was forgotten for 170 years, until redicovered independetly in 1976 by two separate researchers: Eugene Salamin and Richard Brent
p 87: it is

\pi ={\frac {4\left(M(1;{\frac {1}{\sqrt {2}}})\right)^{2}}{\displaystyle 1-\sum _{j=1}^{\infty }2^{j+1}c_{j}^{2}}},

p 92: faster variants have been devleoped, suc as the 1994 Schönhage variant, by Arnold Schönhage
p 94: algorithm, although fast has some complications: (a) uses lots of memory, and complex memory management must be used; (b) high-precision arithmetic is required, so normal computer additon and multi is not sufficient.
p 102: The algorithm was "lost" for 170 years, causign lost opportunity to get more digits out of pi (stuck with the arctan until 1976). HOWEVER even if the algortihm were known, it would have been hard to take advantage of it due to the complexities of full-precision arithmetic. HENCE: the invention of modern computers were necessary to really implement it.
p 102: Num digits from arctan-based algorithsm (before Gause AGM) recror as approx 1M digits in 1976 when AGM rediscovered. Thereafter, that record was shattered ... in just 3 years, it was up to 30million digits.
and it is now the algorithm of choice.

8 Ramanajuan[edit]

p 103: several of R's discoveries are linked with pi; and how to calculate pi
p 103-4: R published an article in 1914 which included 30 formulations for pi, including

{\frac {1}{\pi }}={\frac {2{\sqrt {2}}}{9801}}\sum _{k=0}^{\infty }{\frac {(4k)!(1103+26390k)}{(k!)^{4}396^{4k}}}.

p 104: the R series above was significantly better (converged faster) than previous pi formulae, inclu arctans; about 5x faster than Machin's formula
p 104: that R series was used by Gosper Bill Gosper in 1985 to get 17 million digits.
p 105: that sequence is based on modular equations
p 110: Borwein brothers generalized R's approach, and established a family of series that produce pi.
p 110: Jorg Arndt produced a sequence (from B borthers work) that produces 50 decimal digits of pi each term.
p 110-111: Chudnovsky brothers used a similar sequence to produce pt o 8 billion decicmal digits in 1996: ${\frac {426880{\sqrt {10005}}}{\pi }}=\sum _{k=0}^{\infty }{\frac {(6k)!(13591409+545140134k)}{(3k)!(k!)^{3}(-640320)^{3k}}}\!$

(already in pi article)

p 111: in recent years (?? post 1995?) Ramanujan-link algorithms have been superseded by iterative algorithms developed by the B brothers.
p 111: e.g. the B bros in 1987 came up with a "quintic" iterative algorithm increases the number of digits x5 every iteration!!!
p 111: Howver, these iterative algorithms are related to r's work "... origin can be traced back to R. Thus one can say with some justification that R's hand is still to be foundin pi calculations today".
(not in A book): the iterative techniques (4x or 5x per iteration) were used by Tanaka and others post 2000 to set the world records.

9 Borweins[edit]

p 113: B' brothers are responsible for the algorithms for with pi computations are based today; including David H. Bailey and Kanada.
p 113-114: Bbros first breakthru was in 1984 an iterative algortihm that increased decimal digits 4x each iteration. They based it on the Gauss AGM formula (as it was rediscovered by Eugene Salamin (mathematician) and Richard P. Brent
(no page; from pi article): in 1975 Eugene Salamin (mathematician) and Richard P. Brent discovered (redisocvered the Gauss AGM) approach and came up with an iterative appraoch that doubled the number of decimal digits each iteration.
(no page, not from article) Gauss–Legendre algorithm is the name of the 1975 Brent/Salamin algorithm that doubles the decimal digits each pass
(no page): recap iterative: 1809: Gauss AGM discovered for 1st time; 1975 Salamin/Brent: 2x each pass; 1984: BBros: "quadratic" 4x each pass; 1987: B Bros. "quintic" 5x each pass.
p 115: book by B Brothers:

Pi and the AGM: a study in analytic number theory and computational complexity Volume 4 of Canadian Mathematical Society series of monographs and advanced texts, A Wiley-interscience publication, Authors Jonathan M. Borwein, Peter B. Borwein, Edition reprint, illustrated, Publisher Wiley, 1998, ISBN 047131515X, 9780471315155

p 116: Another book

Pi, a source book, Authors Lennart Berggren, Jonathan M. Borwein, Peter B. Borwein, Publisher Springer, 2004, ISBN 0387205713, 9780387205717

10 BBP "digit extraction algorithm"[edit]

p 117: INvented by Peter B. Borwein, Simon Plouffe and David Bailey
p 117: inventned 1995
formula is already in pi article
hex didgits only
p 126-127: in 1997, Stan Wagon and Viktor Adamchik produced a similar digit extraction algorithm, but simpler. (formula NOT in pi article)
p 128: BBP algorthm (and subsequent similar algorithsm) only produce hex (or octla or binary) digits. No known fast digit extraction alg. that produced decimal digits, yet. Plouffe did create a decimal digit extraction alg, but it is relatively slow (slwoer that full, direct compuation of all pi digits)

11 Fast arithmetic algorithms[edit]

p 131 to execute the modern pi algorthsm in a reasonable amount of time, fast compuer hw alone is not sufficientl. In additoin, special algorithms must be used for arithmetic, in particular, multiplication. NOTE: division and square roots are implemented as a lot of additions & multiplications. A modern pi algoirhtm spends the vast amount of time doing multiplicaitons.
(no page num) see Multiplication_algorithm#Fast_multiplication_algorithms_for_large_inputs for a lsit
p 132: Karatsuba algorithm was an early 1960s (1962 approx) algorithm
(no page nubmer) Toom–Cook multiplication 1963-1966
p 140: 1968: faster FFT_multiplication#Fourier_transform_methods
p 145-6: fast division
p 146-147: fast sqrt
p 149-150: fast nth root
p 150-151: fast series summation: tricks to speed up infinite series compuations; see Series acceleration, e.g. Van Wijngaarden transformation

12 misc[edit]

p 156: Leibnz series is most famouse inf series for pi, but converges very slowly, hence never used.
p 160-161: the first two infinite expressiosn for pi were inf products, not sums! First in 1593 by Francois Veite; 2nd by John Wallis in 1655.
p 161: in 1999 Thomas Osler demonstrated that those two products are closely related

13 History[edit]

greek letter for number

p 165-166: initial use of greek letter pi:
p 165: first used by William Jones in 1706
p 166: however, Jone's work says that that material was copied/originated ith John Machin; so ARndt concludes that Machin actually used the greek letter first.
p 166: the greek letter was used earlier for other circle-related constants, e.g 1631 used by William Oughtred (pi = half circumference of a circle).
p 166: for 30 years (to 1736) no one else used greek letter
p 166: Bernoulli and Euler, prior to 1736 used "c" or "p" for the number
p 166: Euler used pi for the first time in in 1736. He extensively corresponded with other mathemeticieans, so he spread the use around Europe.
p 166: in 1748 Euler published his very widely read Introductio in analysin infinitorum (orig title latin) which used pi and thereafter it use was universal. Quote from that work "For the sake of brevity we will writ ethis number as $π$ ; thus $π$ is equal to half the circumference of a circle of radius 1".

Ancient world

p 165: prehistory: pi assumed to be 3
p 167: Babylon: clay tablet dated 1900-1600 BC has a geometrical statement that, by implication, treats pi as 25/8 = 3 1/8
p 167: Egypt: Rhind Papyrus dated around 1850 BC has a formula for area of circle that treats pi as (16/9)^2
p 168: Egypt: Arndt says there is evidence, speculative, that Etypt may have had accurate polygonal approximations to pi c. 2600 BC
p 168-169: India: Shulba Sutras are ancient Indian math texts in Sanskrit. One from 600BC treats pis as (9785/5568)^2 == 3.088 (not very close). Probably dates to earlier than 600 BC
p 169: India: Probably used sqrt(10) also; a doc from 150 BC uses that. Speculation that sqrt(10) used in India as far back as 500 BC.
p 169-170: BIble: 3; used in two identical verses

Polygons

p 170-171: polygons: first by Archimedes: circa 250 BC: used polgyons to set pi < 22/7 but > 3 10/71 ... very accurate to 3.14
p 171: Archimedes values led to widespread believe that pi = 22/7; based on 96-sided polygons inscribed/circumscribed
P 171: Arndt cites book/paper by Johannes Tropfke on hitory of pi; in german
p 175: Archimedes polygon technique would continue as the primary means of computing pi to be used until 17th century
P 176: Greek astronomer Ptolemy came up with 3.1416 .. not sure of method: probably just enhanced Arch technique

p 176: Rome: No real inteset in pi. Value "3" seems to be used mostly, up to 15 BC

P 176: China: Approx 0 AD, probably had pi around 3.1547
p 176-177: China: around 100AD, sqrt(10)
p 177: China: 3rd c 142/45
p 177: CHina: 263 ad Liu Hui 3.1416 using polygons
p 178: China: Tsu ChlungChih aka Zu Chongzhi circa 480 AD: got to six digits 3.141592; held world record for 800 years; however was not widely known during that period; even in China it was unknown until rediscovered in 14th c.

p 179: India: in 499 AD astonomer Aryabhata in his work Aryabhatiya had value 3.1416. Not clear if he invvented that; or adopted it as an import from Greece/Archimedes.

p 180: Brahmagupta circat 650 AD treated pi with value pi = sqrt(10)
p 180: Fibonacci in circa 1220 had 3.1418 using polygonal method, independent from ARchimedes
p 180: Dante: It is said that he used the value pi= 3 + sqrt(2) / 10
p 180: Dante's Paradise canto XXXIII lines 133-135:

As the geometer his mind applies

To square the circle, nor for all his wit

Finds the right formula, howe'er he tries,

p 182: Persia: Al-Khashi astronomer; got a great results to 16 dec places in circa 1430 using a polgyins with 3 x 2^28 sides. This was world record for about 180 years. Used polygons; but a different algorithm than ARchimedes.

p 182: Francois Viete Dutch? cirac 1579: 9 dec places; used polygon of 3 x 2^17 sides; NOT same as his inf product
p 182: 1593: Dutch Adrian van Romanus 15 de cplaces
p 182: 1596: Dutch Ludolph van Ceulen 32 to 35 dec places; using polygons: 3x2^33 sides
p 183: Hence in Germany sometimes pi was (until WW I ) called "Ludolphian number"
p 183: Wildebrod Snell got to 34 dec digits from 2^30 polygons in 1621
p 183: Christoph Grienberger got to 39 dec places in 1630.

NOTE: all the above use polygon/geometry approaches; except Veite combined with trigonometry

p 184: some iteration (NOT inf series) techniques that anticipated Gausses AGM in 1809
p 184: Gregory: 1667 .. .some polygont stuff
p 184: Descartes 1649: iterative (NOTE: very similar, but not quite as good as later Gause AGM method 160 yrs later)

INIFINITE series

p 185-6: India: date uncertain: noted in 15th c, but could be earlier; Essay by European Charles M. Whish in 1835 was first Eu to document it. India's inf series was at least 100 years before 1st European wich was in 1593.
P 186: Sanskrit docs contain at least 8 series for pi, incl similar to Leibniz series. Attr bio Nilakantha
p 186: series were passed down orally. Hence hard to track originator individual; and details of how derived. Primarily publsiehd by Nilakanthah Somayaji ... probably around 1500.
p 186: Some recent studies show may actual be origianted with Madhavan circa 1400.

p 187: First European inf series by Francois Viete Dutch? in 1593: a product not sum
p 187: John Wallisin 1655 had another product (rathehr famous and elegant) VERY slow convergence
p 188: Brouncker in 1658: first CF for pi (not standard CF)
p 188: Newton and Leibniz independently invented claucalus in 2nd half of 17th centurey: expanding inf series knowlege
p 188: Newton in 1665 or 1666 himself got 15 digits of pi based on an arcsin expansion.
p 188: Newton: "I am ashamed to tell you to how many figures I carried these computations, having no other business at the time". Arndt says this is typical of many pi hunters.
p 188-189: James Gregory did first arctan series in Western world. in 1671. Essentially inventing the Leibniz series.
p 189: Leibniz got the Gregory series independently in 1674. Called the Leibniz series
p 189: First person to use Leibniz series to calculate pi was Abraham Sharp in 1699. Got 71 terms. FIRST WORLD record _not_ based on polygons.
p 190-191: Euler came up with many formulae involving pi, including the famous Euler identity in 1743
p 191: Another key equation discovered by Euler (alreday in pi article) was pi^2 / 6 = sum of ( 1 / k^2 ) in 1736

ARCTAN

p 192: John Machin invents the 15 atan(1/5) - 4 atan(1/239) = pi formula in 1706. First mathematicain to combine two arctans into one formula. He got 100 digits.
p 193: Machin did not publish his result (formula or 100 digits) it was pubished by William Jones - including use of "pi" for first time ... perhaps due to Machin not Jones
P 193: Machins algorithm was the best & used for 200 years ... although some developed variants of it, especially Gauss

p 194: Japan: Takebe Kenko 1722 - 41 dec digits of pi^2
p 194: Japan: Matsunaga 1739: 50 dec plces

p 194: Austria: Zacharias Dase in 1840: 200 digits (using arctan) ... amazing human calculator!!
p 195-196: England William Shanks 1851 to 1853: 500 to 700 digits; but contained some mistakes. ... got 530 correct

p 196: 1882: pi is transcental -> cannot construct with compass & straightedge; by Ferdinand Lindemann
p 197: 1945 to 1949: final record set by hand (w/o computers): by John Wrench Jr. and Daniel Fergeson: 1,120 digits

Computer era

p 197: 1949 ENIAC in 1949: 2,037 digits .. 70 hours ... arctan
p 197: 1957 F. E. Felton 7,480 digits ... arctan
p 197: 1958: 10,000 digits F. Gunuys ... arctan
p 197: 1961: 100,000 digits John Wrench Jr. and Daniel Shanks ... arctan
p 197: NOTE: verify results by using a 2nd algorithm: this is key: every modern hunter must use TWO algortihms to validate. This ocmputer era they always used two different arctan formulae; but both were arctan.
p 197: 1973; 1M digits

Breakthru

p 198-200: stagnatn at 1M digits until 1980s, then two things happend:

Fast multiplication, esp FFT multp

redicsovery of iterative approaches: Gaus AGM & Ramanujans series;the AGM doubled number of digits each iteration

p 200: thus, from 1981 to 1999, the record was broden 26 times; often by doubling previous
p 113-114: e.g Borwien brothes 4x iterative algorithm (basedon AGM) in 1984
p 200-201: Kanada: secritive
P 201-202: Chudnovsky brothers: odd, hermits, NY, strange story

Single Digits

p 203: "The 2000 year search for ever more pi digits is changing direction" due to the BBP algorithm for digit extraciton
p 203: 1995: 10 billionth hex digit (approx twice as far into pi as the contemporary full-digit record of the time)
p 203: 1997: Fabrice Bellard student modifies BBP and gets 250 billionth hex digit
P 203: 2000: 250 trillionth hex digit: 19 year old Colin Percival ... using Bellard's modification to BBP .. using pihex program

14 Misc[edit]

p 211: pyramids in Egypt: speculation that dimensions are related to pi: cheops pymrd: 2xbase : height == 22:7 == pi approx ... but this is very speculative
p 211-2: 1897 Indiana pi law Indiana Pi Bill

Posamentier: A biography of ...[edit]

outline[edit]

p 15: pi is 16th letter of greek alphabet
p 21: 2002: Kanada 1.24 trillion dec digits; 600 hrs of computer time
p 21: why get so many digits? Answer: no reason for pi to have so many. Proactical benefis are: testing computer; testing algorithms; testbed for optmizations, etc
p 24: archimedes 223/71 < pi < 22/7
p 25: Transendence in 1882 by Lindemann: proved impossible to square the circle
p 27-28: Bible: 1 Kings 7:23 and 2 Chronicles 4:2 Molten Sea : 10 cubits across; 30 cubits circumference
p 29: who chose greek letter pi? 1706 W. Jones; but 1736 usage & esp 1748 publ by Euler reall made it famous
p 36-37: Indiana pi law
p 38-39: needle tossing Buffon
p 42-44: Egypt; Rhind papyrus
P 44: Babylon: 200 to 600 BC: 3 1/8
p 45: bible: 3
p 52 - 55 ARchimedes: p between 3 10/71 and 3 1/7 (acc to 3.14)
p 60: Ptolomey: pi = 3 17/120 == 3.1416
p 61: China: Liu Hui: 263 AD 3,927 / 1250 = 3.1416
p 62: Fibonacci
p 63: artist Albrecht Durer circa 1500 used 3 1/8.
p 63: Viete: inf multip seq
p 64: Ludolph van Ceulen 1596: 20 dec places using polgyons
p 64: Wallis: 1655: inf product for pi
p 65: Brouncker: converted Wallis product into a CF (non simple)
p 67: WIlliam Jones 1706: "pi" as ratio; no mention of Machin; 1748: Euler popularizes when publ the IIAI book
p 68: Euler 126 places
p 69: Gauss employed Dahse using a 3-term arctan algorithm: 200 places
p 70: Claussen 1874 248 places; Ruherford 1853: 440 dec places; Shanks 527 places (707 but for error)
p 70: Shanks took 15 years!! for his calculation
p 70: Lindemann: transcend proof
p 71: Ramanujan
p 72: ENIAC 2037 places 1949.
p 73: Chudnovsky brothers: MacArthur Foundation fellowship
p 74: big purpose of pi digit hunting now is to test computers & algorithsm
p 80-90: explains Archimedes polygon method
p 102-104: Graphical method (count lattice pts/squres in a figure ... not mentioned in Arndt)
p 105-108: Monte carlo
p 109-111: Inf series sums
p 112-116: Ramanujan algorithms

more[edit]

p 118: "pi room" in palais Decourvert
p 118: pi day march 14
p 122: Mnemonics & memorization
p 123-7: other languages
p 129-133: randomness
p 137-8: coincicens: digits in certain locations
p 139: probabiliy: 6/pi^2 = probl that 2 numbers are relatively prime;

ALSO the probl that a random numer has "no repeated prime divisors". (Not in ARndt)

p 140-141: river meandering: formula invovles pi; very sketchy & hypothetical
p 142-144: More coincidences: fractions/products/etc very near pi
p 146-152: CF

applications[edit]

p 170-171: sports track: where to draw the starting lines to ensure each runner runs same distance (and finiehs at a single fiish line)
p 222-237: Ring around the equator paradox

List of persons associated with pi[edit]

Plato Newton J. Von Neuman Euler Archimedes Ramanujan Sagan ? Martin Gardner Dante Gauss

U. Eco: Focault's pendulum; p 3 Ballantine, 1988. Cited by "Pi: A Sourcebook" p 658.

Source Book[edit]

p 642-647: 1989 B , B & Dilcher: analyssis of slowly convergent Gregory Seriies: after 500,000 terms, it is correct to only 5 places; but it is correct in 36 of the first 40 places. Only wrong digits are 6, 17, 18, and 29.

sources[edit]

Secondary / survey sources

The Joy of Pi David Blatner - Walker & Co - 1999 - 144 pages

Pi : a Source Book Lennart Berggren, Jonathan Borwein, Peter Borwein - Springer Verlag - 1997 - 736 pages

History of Pi Peter Beckman - St. Martin's Press - 1976 - 200 pages

Pi Unleashed j. Arndt et C. Haenel - Springer - 2006 - 269 pages

Sir Cumference and the Dragon of Pi : A Math Adventure Cindy Neuschwander, Wayne Geehan - Charlesbridge Publishing - 1999 - 32 pages

- childrens comic book

A History of the Circle : Mathematical Reasoning and the Physical Universe Ernest Zebrowski - Rutgers Univ Press - 1999 - 215 pages

Pi and the AGM P. Borwein et J. Borwein - Wiley - 1987 - mentioned by Arndt in ch 12

The Number Pi P. Eymard/J.P. Lafon - Hermann/AMS - 1999 - 318 pages

H.C. Schepler, The Chronology of Pi. Mathematics Magazine 23(1950) 165-170, 216-228, and 279-283

Primary/original sources

K. Mukunda Matar and C. T. Rajagonal, On the Hindu Quadrature of the Circle. Appendix by K. Balagangadharan. Journal of the Bombay Branch of the Royal Asiatic Society 20(1944) 77-82

H. Engels, Quadrature of the Circle in Ancient Egypt., Historia Mathematica 4(1977) 137 - 140

T. L. Heath, The Works of Archimedes with the Method of Archimedes. Dover Publications Inc., New York 1953, pp. 91-98

Lam Lay-Yong and Ang Tian-Se, Circle Measurements in Ancient China. Historia Mathematica 13(1986) 325-340

F. Viete, Variorum de Rebus Mathematicis Reponsorum Liber VII. F. Viete, Opera Mathematica (repr.). Georg Olms Verlag, Hildesheim, New York 1970, pp. 398-401, 436-446

J. Wallis, Arithmetica Infinitorum, sive Nova Methodus Inquirendi in Curvilineorum Quadratum, aliaque difficiliora Matheseos Problemata. Oxford 1655/6. Reprinted in vol. 1 (pp. 357-478) of Opera Mathematica. Oxford 1693

C. Huygens, De Circuli Magnitudine Inventa. Christiani Hugenii Opera Varia I. Leiden 1724, pp. 384-388

Ranjan Roy, The Discovery of the Series Formula for p by Leibniz, Gregory, and Niakantha. Mathematics Magazine 63(1990) 291-306

L. Euler, On the Use of the Discovered Fractions to Sum Infinite Series. L. Euler, Introduction to Analysis of the Infinite. Book I. Translated from the Latin by J. D. Blanton. Springer-Verlag, New York 1964, pp. 137 - 153

W. Shanks, Contributions to Mathematics Comprising Chiefly of the Rectification of the Circle to 607 Places of Decimals. London 1853, pp. i-xvi, 10

F. Lindemann, Ueber die Zahl pi. Mathematische Annalen 20(1882) 213-225

S. Ramanujan, Modular Equations and Approximations to pi. Journal of the Indian Mathematical Society, XLV, 1914, 350-372 G.H. Hardy, P.V. Sehuigar, and B. M. Wilson (eds), S. Ramanujan: Collected Papers. Chelsea, New York 1962, pp. 23-29

I. Niven, A Simple Proof that pi Is Irrational. Bulletin of the American Mathematical Society, vol. 53, no. 7, July (1947), p. 507

G.W. Reitwiesner, An ENIAC Determination of pi and e to 2000 Decimal Places. Mathematical Tables and Other Aids to Computation 4(1950) 11-15

. D. Shanks and J. W. Wrench, Jr, Calculation of pi to 100,000 Decimals. Mathematics of Computation 16(1962) 76-99

D.A. Cox, The Arithmetic-Geometric Mean of Gauss. L' Ensignement Mathematique 30(1984) 275-330

J.M. Borwein and P. B. Borwein, The Arithmetic-Geometric Mean and Fast Computation of Elementary Functions. SIAM Review 26(1984) 351-365

S. Wagon, Is Pi Normal? The Mathematical Intelligencer 7:3(1985) 65-67

D.V. Chudnovsky and G.V. Chudnovsky, Approximations and Complex Multiplication According to Ramanujan. G.E. Andrews et al (eds), Ramanujan Revisited. Academic Press, Boston 1988, pp. 375-396, 468-472

J.M. Borwein, P.B. Borwein and D.H. Bailey, Ramanujan, Modular Equations, and Approximations to Pi or How to Compute One Billion Digits of Pi. The American Mathematical Monthly 96(1989) 201-219

refs[edit]

^ Barrow, John D (2002). The Constants of Nature. London: Jonathan Cape. ISBN 0-224-06135-6.

[1] Barrow, John D (2002). The Constants of Nature. London: Jonathan Cape. ISBN 0-224-06135-6.

[1]